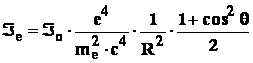 , (1)
, (1)Поскольку кристаллические структуры есть периодические, то очевидно возможна дифракция волн при прохождении их через вещество в соответствии с общими принципами дифракции. Параметр кристаллической решетки порядка 10-10м, следовательно, формировать дифракционную картину могут волны с длинами волн λ ~ 10-10 м, сравнимые со средним межатомным расстоянием. Этому условию удовлетворяют рентгеновские лучи, электронные и нейтронные пучки определенной энергии. Дифракция рентгеновских лучей (рентгенография), дифракция нейтронов (нейтронография) и дифракция электронов (электронография) – наиболее распространенные методы исследования структуры большинства твердых тел, обеспечивающие получение информации об атомной структуре твердых тел как кристаллических, так и аморфных.
Интенсивность рассеяния электронов на 6-7 порядков выше, чем фотонов и нейтронов. Сильное взаимодействие электронов с веществом ограничивает толщину исследуемых в геометрии на просвет объектов (тонкие пленки ~10-50 нм). Особенностью дифракции в геометрии на отражение является малая глубина проникновения электронного пучка и, следовательно, большое влияние неоднородностей поверхности. Таким образом, информация о структуре, получаемая электронографически, ограничивается тонкими слоями.
Структурная нейтронография во многом похожа на рентгеноструктурный анализ. Отличия связаны с тем, что нейтроны рассеиваются ядрами, а рентгеновские лучи –электронными оболочками атомов. Нейтронография применяется для решения задач, малодоступных для рентгеновского анализа, таких как определение присутствия водорода, анализ соединений атомов с близкими атомными номерами, соединений легких атомов с тяжелыми. Характерными особенностями метода является большая проникающая способность нейтронов и широкий диапазон длин волн.
Длина волны для таких частиц как He2, D2, HD, Ne, He при энергии 0.01-0.1 эВ приближается к величине межатомных расстояний (~0.1 нм), что и обеспечивает дифракцию. При таких энергиях метод дифракции атомных и молекулярных пучков (ДАМП) является неразрушающим и дает информацию только о внешней поверхности. Наиболее широко ДАМП используется сейчас для изучения адсорбционных слоев на чистых поверхностях. Основные трудности метода связаны с необходимостью учета неупругих и многократных столкновений.
Рентгеновский фотон слабо взаимодействует с атомами и поэтому испытывает только однократные столкновения. С этим связана высокая проникающая способность таких фотонов, что не позволяет использовать их для диагностики периодической структуры тонких приповерхностных слоев кристаллов. Ситуация несколько изменится, если использовать скользящие лучи (угол к поверхности меньше 0.1 мин) и монохроматическое рентгеновское излучение. Особенно эффективны для этих целей источники синхротронного рентгеновского излучения.
Очень просто и изящно истолковали интерференцию рентгеновских лучей в кристаллах русский ученый Ю.В.Вульф (1912) и независимо от него английские физики отец и сын Г. и Л. Брэгги (1913), объяснив это явление их «отражением» (как от зеркала) от атомных плоскостей. Основываясь на этих соображениях, они вывели формулу, описывающую положение интерференционных максимумов, известную как формулу Вульфа-Брэггов. Эта формула является следствием основного свойства кристалла – периодичности его структуры и не связана ни с химическим составом кристалла, ни с расположением атомов в отражающих плоскостях. Эти факторы влияют на величину интенсивности максимумов.
Интенсивность рефлексов при рентгеновской дифракции на практике определяется с достаточной степенью точности количественно. На интенсивность влияет ряд факторов, вклад которых можно оценить теоретически. Рассмотрим эти факторы последовательно. Для количественной оценки взаимодействия рентгеновского излучения с кристаллом воспользуемся результатами классической электродинамики. Квантовые эффекты, как правило, участвуют в создании некогерентного рассеяния и флюоресценции, которые вносят вклад в интенсивность фона и могут быть исключены теоретически и экспериментально.
При падении на электрон плоской монохроматической волны рентгеновского излучения электрическое поле волны приводит электрон в колебание с частотой самой волны. Колеблющийся электрон, являющийся диполем с переменным электрическим моментом, создает, в свою очередь, переменное электрическое поле. Интенсивность этого поля и есть интенсивность излучения, рассеянного электроном. Из электродинамики известно, что для рентгеновского луча, рассеиваемого электроном (свободным или слабосвязанным) под углом 2θ к падающему лучу в точке А, находящейся на расстоянии R от электрона, интенсивность определяется как
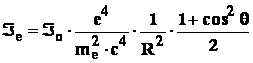 , (1)
, (1)
где е – заряд, me – масса электрона, с – скорость света, ![]() – интенсивность первичного луча.
– интенсивность первичного луча.
Величина P = (1 + cos2θ)/2 в рентгеноструктурном анализе получила название поляризационного фактора, который для каждого дифракционного максимума может быть легко найден по брэгговскому углу θ.
Очевидно, что интенсивность рентгеновского отражения должна быть пропорциональна рассеивающей способности атома в кристаллической решетке. Рентгеновские лучи рассеиваются электронными оболочками атомов. Если ввести функцию распределения электронной плотности атома ρ(r) и предположить, что она сферически симметрична и простирается от 0 до ∞, то расчеты приводят к следующему выражению для амплитуды суммарной волны, рассеиваемой атомом
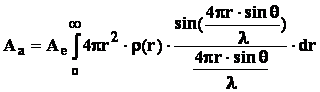 , (2)
, (2)

где Ае – амплитуда волны, рассеянной одним электроном.
Число, показывающее во сколько раз эта амплитуда больше амплитуды волны, рассеиваемой электроном, при тех же условиях, есть атомный фактор рассеяния f некоторого атома, т.е.
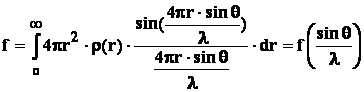 . (3)
. (3)
При малых значениях sinθ/λ фактор атомного рассеяния f = Z, где Z - число электронов в атоме (рис.1).
Таким образом, атомный фактор есть функция аргумента sinθ/λ и его вид определяется радиальным распределением электронов в сферически симметричном поле. Значения атомного фактора при различных sinθ/λ протабулированы для всех атомов и ионов.
Формула Вульфа-Брэггов определяет отражения (hkl), возможные для данной кристаллической решетки, но не позволяет сделать заключение о величине относительных интенсивностей различных отражений, которая зависит от характеристик элементарной ячейки, т.е. от типа ячейки, от числа и расположения атомов в ней. Если элементарные ячейки каких либо различных веществ подобны по форме и тождественны по размерам, то геометрическое расположение рефлексов на рентгенограммах всегда совершенно одинаково, независимо от того содержит ячейка один, два или большее число атомов. Материальному различию приведенных структур отвечает резкое различие интенсивностей геометрически тождественных рефлексов, которое обусловлено различием рассеивающих способностей атомов, входящих в состав элементарной ячейки.
Структурная амплитуда – это амплитуда волны, рассеянной в данном направлении всеми атомами элементарной ячейки. Она обычно выражается в электронных единицах, т.е. по отношению к интенсивности рассеяния одним электроном. Таким образом, каждому отражению (HKL) соответствует своя структурная амплитуда. Если fn – атомный фактор рассеяния n-го атома элементарной ячейки, то структурная амплитуда, являющаяся суперпозицией всех отдельных лучей, полученных при рассеянии на атомах ячейки, определится как
![]() , (4)
, (4)
где Fn – разность фаз для лучей, рассеянных на n-ом атоме и атоме, расположенном в начале координат.
Можно показать, что
![]() , (5)
, (5)
где xn, yn, zn – координаты n-го базисного атома в элементарной ячейке, N- число атомов базиса. Выражение для структурной амплитуды с помощью формулы Эйлера может быть записано в иной форме
![]() (6)
(6)
А интенсивность отраженных от элементарной ячейки кристалла лучей будет определяться так называемым структурным фактором, равным квадрату модуля структурной амплитуды.
![]() . (7)
. (7)
На структурном факторе (амплитуде) сильно сказываются кристаллографические особенности кристаллической структуры: ее элементы симметрии, тип решетки. Структурный фактор (амплитуда) есть безразмерная величина, характеризующая только кристаллическую структуру.
При расчете структурного фактора его формулу сначала упрощают для заданных HKL, а затем подсчитывают Hxn+ Kyn+ Lzn, для атомов базиса, после чего рассчитывают значения косинусов и синусов, суммируют их, умножают на соответствующее значение атомного фактора и суммируют полученные частные суммы.
Вывод выражения для атомного фактора был сделан в предположении о покоящемся атоме со сферически распределенной электронной плотностью. В реальном кристалле атомы, а значит и электроны, совершают хаотические тепловые колебания около положений равновесия, кроме того, между атомами существуют определенные химические связи. Тепловое движение оказывает влияние на значение рассеивающей способности атома, а, следовательно, и на интенсивность рефлексов. Температурный множитель учитывает разность фаз рассеянных лучей, возникшую вследствие тепловых колебаний. Изменение интенсивности отражений, обусловленное тепловым движением атомов определяется формулой
![]() , (7)
, (7)
где ![]() – интенсивность, вычисленная без учета тепловых колебаний,
– интенсивность, вычисленная без учета тепловых колебаний, ![]() – истинная интенсивность,
– истинная интенсивность,
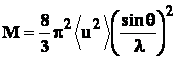 ,
,
где <u2> - среднеквадратичное смещение атомов из положения равновесия. Фактор W=е-2М носит название фактора Дебая-Валлера.
Смещение атомов из идеальных положений может возникать не только под влиянием тепловых колебаний. Вследствие различия в размерах атомов, составляющих кристалл, и наличия химической связи между атомами также может возникать дополнительное смещение атомов.
Фактор повторяемости р равен числу атомных плоскостей кристалла, принимающих участие в создании данного рефлекса на рентгенограмме. Т.е. р равен числу семейств плоскостей, имеющих одинаковое межплоскостное расстояние и одинаковый структурный фактор.
Фактор поглощения А(θ) учитывает ослабление лучей в образце при данной геометрии рентгенографирования и зависит от угла падения θ, плотности вещества и линейного коэффициента поглощения μ. Однако можно выбрать толщину образца такой, чтобы А не зависел от угла θ и соответственно не вносил вклада в относительную интенсивность. Поэтому чаще всего полагают А=1.
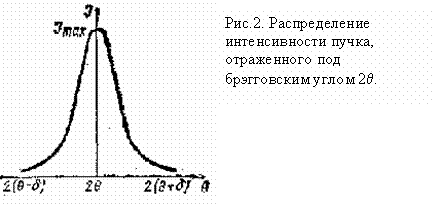
Реальные кристаллы являются мозаичными, т.е. состоят из блоков, повернутых друг относительно друга на малые углы. По этой причине кристалл отражает не только под брэгговским углом, но и в некотором угловом интервале (рис.2).
По этой причине при теоретическом подсчете интенсивностей надо вычислять не максимальное значение интенсивности брэгговского пика, а интегральную величину в пределах углов, при которых еще происходит отражение. Для учета влияния на интенсивность отраженных лучей мозаичности кристалла, а также геометрии рентгенографирования при расчете интенсивности вводят фактор Лоренца L, который для поликристаллов равен
![]() . (8)
. (8)
С учетом всех выше рассмотренных факторов относительные интегральные интенсивности дифракционных максимумов рассчитываются как
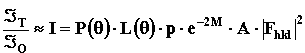 . (9)
. (9)
Задание: Рассчитать относительную интенсивность линий рентгенограммы поликристаллического вещества, полученной с помощью монохроматического рентгеновского излучения.
![]() , где а – постоянная решетки кубического кристалла.
, где а – постоянная решетки кубического кристалла.
Таблица1. Индексы интерференции первых десяти линий рентгенограммы
Номер линии в порядке возрастания углов |
Объемоцентрированная кубическая решетка |
Гранецентрированная кубическая решетка |
||
H2+K2+L2 |
HKL |
H2+K2+L2 |
HKL |
|
1 |
2 |
110 |
3 |
111 |
2 |
4 |
200 |
4 |
200 |
3 |
6 |
211 |
8 |
220 |
4 |
8 |
220 |
11 |
311 |
5 |
10 |
310 |
12 |
222 |
6 |
12 |
222 |
16 |
400 |
7 |
14 |
321 |
19 |
331 |
8 |
16 |
400 |
20 |
420 |
9 |
18 |
411,330 |
24 |
422 |
10 |
20 |
420 |
27 |
333,511 |
№ линии |
HKL |
d, Å |
sin θ |
p |
P × L |
sin θ/λ |
fn |
Fhkl 2 |
I |
I отн, % |
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы